

 |
 |
We give coordinate-minimal geometric realizations in general position for 17 of the 20 vertex-minimal triangulations of the orientable surface of genus 3 in the 5x5x5-cube.
By Heawood's inequality from 1890 [10], every triangulation of a (closed) surface M of Euler characteristic chi(M) has at least
n ≥ 1/2(7+sqrt(49-24*chi(M)))
vertices. The tightness of this bound was proved by Jungerman and Ringel [15] for all orientable surfaces (with the exception of the orientable surface of genus 2, where an extra vertex has to be added [14]). The first known vertex-minimal triangulation of the orientable surface of genus 3 with 10 vertices can be found on p. 23 in the book of Ringel on the Map Color Theorem [18].
A complete enumeration of all 42426 triangulated surfaces with 10 vertices was obtained in [16]; see [17] for a list of facets (in mixed lexicographic format as well as in lexicographic format) and [20] for an isomorphism free lexicographic enumeration of the triangulations with up to 12 vertices. In particular, there are exactly 20 combinatorially distinct vertex-minimal 10-vertex triangulations of the orientable surface of genus 3.
By Steinitz' theorem (cf. [21, Ch. 4]), every triangulated 2-sphere is realizable as the boundary complex of a convex 3-dimensional polytope. For orientable surfaces of genus g ≥ 1 Grünbaum [9, Ch. 13.2] asked whether triangulations of these surfaces can always be realized geometrically as polyhedra in R3, i.e., with straight edges, flat triangles, and without self intersections? In general, the answer turned out to be "No": Bokowski and Guedes de Oliveira [5] showed that there is a non-realizable triangulation of the orientable surface of genus g = 6. Recently, Schewe [19] extended this result and proved that there are non-realizable triangulations for all orientable surfaces of genus g ≥ 5. For surfaces of genus 1 ≤ g ≤ 4 the problem remains open.
The realizability problem for triangulated surfaces is decidable (cf. Bokowski [1] and Bokowski and Sturmfels [6, Ch. VIII]), but there is no deterministic algorithm known that would solve the realization problem for instances with as few as, say, 10 vertices in reasonable time.
Geometric realizations for several examples of triangulated orientable surfaces of genus 2, 3, and 4 with respective minimal numbers of vertices 10, 10, and 11 were constructed by Bokowski and Brehm [3], [4] and Brehm [7], [8]. In particular, Brehm [7], [8] and Bokowski and Brehm [3] gave polyhedral models for five combinatorially different 10-vertex triangulations of the orientable surface of genus 3; see below for more details on these five examples.
Geometric realizations for all 865 vertex-minimal 10-vertex triangulations of the orientable surface of genus 2 were obtained by Bokowski [2] and Lutz [16], based on a random search procedure and geometric intuition; see also [11]. With a simulated annealing approach [12], it was also possible to realize all 20 examples of genus 3 with 10 vertices (as well as all 821 vertex-minimal triangulations with 11 vertices of the orientable surface of genus 4).
Theorem (Hougardy, Lutz, and Zelke [12]): All 20 vertex-minimal 10-vertex triangulations of the orientable surface of genus 3 can be realized geometrically in R3.
For most of these examples there even are realizations with rather small coordinates.
Theorem: At least 17 of the 20 vertex-minimal 10-vertex triangulations of the orientable surface of genus 3 have realizations in general position in the 5x5x5-cube, but none of the 20 triangulations can be realized in general position in the 4x4x4-cube.
To obtain this result, we completely enumerated for increasing n all sets of 10 vertices in general position in the nxnxn-cube that are compatible with a given triangulation; cf. [11] and [13]. To speed up this enumeration we made use of the symmetry of the nxnxn-cube, enumerated only lexicographic minimal vertex sets, and checked compatibility with a given triangulation for partially generated vertex sets. The search for realizations in the 5x5x5-cube was run (in total) for 2 CPU years on a 3.5 GHz processor. Hereby, roughly 1/5th of the possible vertex sets in the 5x5x5-cube was processed.
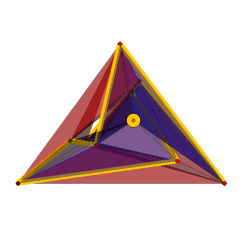
The displayed example Polyhedron_2_10_14542 has one clearly visible hole, while all other tunnels are hidden. In the transparent display of the polyhedron we have highlighted the link of a vertex. The number 14542 indicates the position of the example in the catalog of the 42426 triangulated surfaces with 10 vertices in mixed lexicographic format from [17]. The attached archive Polyhedra_Genus-3_Vertices-10_Format-obj.tar.gz contains the coordinates for the 17 coordinate-minimal examples (one of which was found by coordinate recycling) as well as coordinates obtained in [12] for the remaining 3 examples in obj-format.
Of the 20 examples, 8 have only trivial combinatorial symmetry, 3 examples have Z2-symmetry, and 4 have Z3-symmetry. Further, there are 2 with Z4-, 1 with Z2xZ2-, 1 with A4-, and 1 with Z7xZ3-symmetry. The symmetry groups of the examples are contained in the archive Polyhedra_Genus-2_Vertices-10_Format-other.tar.gz.
In general, the geometric symmetry group of a polyhedral surface can be smaller than its combinatorial symmetry group. For example, the geometric symmetry group of a polyhedron of genus 3 with 10 vertices is of order at most 4 [8], while the example 28399 has the combinatorial symmetry group A4 of order 12 (cf. [3]) and the example 29173 has the combinatorial symmetry group Z7xZ3 of order 21.
A polyhedral realization of the example 10368 was first found by Brehm [7] along with a modification that gives a realization of the example 10341. The example 28399 was first realized by Bokowski and Brehm [3] and the example 27718 by Brehm [8] together with a slight modification that yields a realization of the example 11250.
Acknowledgement: The first and the third author were supported by the DFG Research Center MATHEON "Mathematics for Key Technologies", Berlin, the second author was supported by the DFG Research Group "Polyhedral Surfaces", Berlin.
| Keywords | triangulated surface; polyhedral realization; small coordinates | |
| MSC-2000 Classification | 52B70 (57Q15) | |
| Zentralblatt No. | 05264904 |
Submitted: Mon Feb 13 15:02:48 MET 2006.
Revised: Mon Mar 12 15:34:00 MET 2007.
Accepted: Tue Mar 20 12:07:00 MET 2007.
Humboldt-Universität zu BerlinFrank H. Lutz
Institut für Informatik
Unter den Linden 6
10099 Berlin
Germany
hougardy@informatik.hu-berlin.de
http://www.informatik.hu-berlin.de/~hougardy/
Technische Universität BerlinMariano Zelke
Fakultät II - Mathematik und Naturwissenschaften
Institut für Mathematik, Sekr. MA 3-2
Straße des 17. Juni 136
10623 Berlin
Germany
lutz@math.tu-berlin.de
http://www.math.tu-berlin.de/~lutz
Humboldt-Universität zu Berlin
Institut für Informatik
Unter den Linden 6
10099 Berlin
Germany
zelke@informatik.hu-berlin.de
http://www.informatik.hu-berlin.de/~zelke/