Triply Periodic Discrete Schwarz P-Surface

Authors

Description

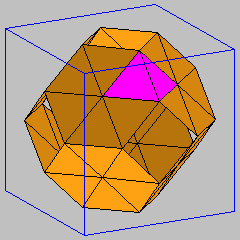
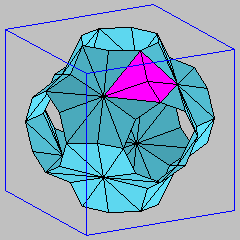
These are the two simplest triply periodic discrete minimal surfaces with the same symmetry group as the smooth minimal Schwarz p-surface. By reflection in the planar symmetry lines these models extend to triply periodic discrete minimal surfaces. For both discrete surfaces, a fundamental piece for the translational symmetry group sits in a cube, which is shown in the figures together with another configuration consisting of four fundamental pieces.

We define discrete compact minimal surfaces as piecewise linear continuous compact triangulated surfaces that are critical for the area functional with respect to all variations through surfaces of the same type that preserve the simplicial structure and the boundary condition (see [2] and model [5] on this server).

The two examples (Schwarz1 and Schwarz2) shown here fulfill the discrete minimality conditions since:

• the surfaces have a great deal of symmetry, and
• there exist fundamental pieces of the surfaces consisting of two triangles from which the entire surfaces can be built using only 180 degree rotations about edges and reflections across planes.

The two models are analogous to the well-known smooth minimal Schwarz P-surface. The first two figures show two assemblings of the simplest possible discrete minimal "Schwarz" surface (Schwarz1): the first picture exhibits the surface in the cubical 3-torus formed by translational symmetries of the surface, and the second model shows how the parts combine to form an infinite periodic boundary-free discrete minimal surface in Euclidean 3-space. The last two figures show another discrete minimal "Schwarz" surface (Schwarz2), whose mesh is topologically a subcomplex of the previous model (Schwarz1), in two similar assemblings as the first model (Schwarz1). Both models are described in detail in [1].

Model produced with: JavaView v. 2.04.001

References

1. Konrad Polthier and Wayne Rossman: Index of Discrete Constant Mean Curvature Surfaces (2000), Preprint 484, submitted, http://www-sfb288.math.tu-berlin.de/~konrad/articles.html.
2. Ulrich Pinkall and Konrad Polthier: Computing Discrete Minimal Surfaces and Their Conjugates, Experimental Mathematics 2 (1993), 15--36.
3. Bernd Oberknapp and Konrad Polthier: An Algorithm for Constant Mean Curvature Surfaces, in Hans-Christian Hege and Konrad Polthier (Eds.): Visualization and Mathematics, Springer Verlag (1997), 141--161.
4. Konrad Polthier and Samy Khadem and Eike Preuss and Ulrich Reitebuch: JavaView Home Page, http://www.javaview.de/.
5. Konrad Polthier and Wayne Rossman: Discrete Catenoid (2000), Digital Model at Electronic Geometry Models, http://www.eg-models.de/2000.05.002.

Files

• Master File: Schwarz1Single_Master.jvx
• Master File: Schwarz1Multiple_Master.jvx
• Master File: Schwarz2Single_Master.jvx
• Master File: Schwarz2Multiple_Master.jvx
• Applet File: Schwarz1Single_Applet.jvx
• Applet File: Schwarz1Multiple_Master.jvx
• Applet File: Schwarz2Single_Applet.jvx
• Applet File: Schwarz2Multiple_Master.jvx
• Preview: Schwarz1Single_Preview.gif
• Preview: Schwarz1Multiple_Preview.gif
• Preview: Schwarz2Single_Preview.gif
• Preview: Schwarz2Multiple_Preview.gif
• Other: Schwarz1Single_Display.jvd
• Other: Schwarz2Single_Display.jvd

Submission information

Submitted: Mon Jan 22 09:21:14 CET 2001.
Revised: Fri Jul 20 11:13:14 CET 2001, Mon Aug 27 21:41:30 CET 2001, Mon Sep 10 12:17:19 CET 2001.
Accepted: Tue Sep 11 15:21:41 CET 2001.

Authors' Addresses

Technische Universität Berlin
Fachbereich Mathematik
Straße des 17. Juni 136
10623 Berlin
Germany
polthier@math.tu-berlin.de
http://www-sfb288.math.tu-berlin.de/~konrad

Kobe University
Mathematics Department
Faculty of Science
Rokko, Kobe 657-8501
Japan
wayne@math.kobe-u.ac.jp
http://www.math.kobe-u.ac.jp/HOME/wayne/wayne.html