Bubbletons and their parallel surfaces in Euclidean 3-space

Author

Description

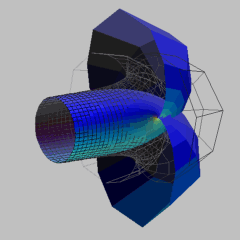
We show one of the cylinder bubbletons in Euclidean 3-space, which are constant mean curvature surfaces (we choose the mean curvature to be 1/2) derived by applying the Backlund-Bianchi transformation to the cylinder. We also show the parallel constant mean curvature surface of this cylinder bubbleton. The simplest cylinder bubbletons are congruent to their parallel constant mean curvature surfaces, as in the figure shown here.

Bubbletons in Euclidean 3-space have been closely examined in [3]. In this model, we show a bubbleton surface in Euclidean 3-space that was computed using the DPW method [1]. The surface is shaped like a cylinder with attached bubbles, thus it is called a bubbleton.

The parallel constant positive Gaussian curvature surface of the bubbleton is well known and was first found by Sievert, thus it is called the Sievert surface.

With respect to the DPW method (see [1]), the Backlund transformation is a dressing action on loop groups and this dressing action is described by elements of the simplest possible type like those of Terng and Uhlenbeck [4].

Using these elements, we can compute explicit parametrizations for the cylinder bubbletons and their parallel surfaces, and furthermore conclude that 1) the simplest of these surfaces are congruent to their parallel surfaces, and 2) these surfaces are the same as those found in [3]. (These bubbletons in Euclidean 3-space have also been constructed by Nick Schmitt using the CMC Lab software, see [2].) Detailed proofs of these facts can be found in the postscript, pdf and Mathematica files included in this model. Basic introductory material is also included in these files. The specific parameters used to compute the Master model files are described in the Mathematica files.

Model produced with: JavaView v.2.13.002

References

1. J. Dorfmeister, F. Pedit and H. Wu: Weierstrass type representation of harmonic maps into symmetric spaces, Comm. Anal. Geom. 6, 4 (1998), 633--668, .
2. N. Schmitt: CMCLab software, http://www.gang.umass.edu/gallery/cmc.
3. I. Sterling and H. C. Wente: Existence and classification of constant mean curvature multibubbletons of finite and infinite type , Indiana U. Math. J. 42, 4 (1993), 1239--1266, .
4. C.-L. Terng and K. Uhlenbeck: Backlund transformations and loop group actions, Comm. Pure and Appl. Math. 53 (2000), 1-75, .

Files

• Master File: R3bubbleton.jvx
• Applet File: R3bubbleton.jvx
• Preview: R3bubbleton.gif
• Other: R3bubbleton.nb
• Other: bubbleton.pdf
• Other: bubbleton.ps

Submission information

Submitted: Mon Mar 4 02:46:04 GMT 2002.
Revised: Tue Oct 1 14:50:15 CEST 2002, Mon Jan 6 17:23:03 GMT 2003.
Accepted: Fri Feb 14 18:06:11 CET 2003.

Author's Address

Kobe University
Mathematics Department
Faculty of Science
Rokko, Kobe 657-8501
Japan
kobayasi@math.kobe-u.ac.jp
http://www.math.kobe-u.ac.jp/~kobayasi