

 |
 |
 |
 |
In 1958 Mary Ellen Rudin [5] gave a construction of a non-shellable triangulation of a 3-ball having f-vector (14,66,94,41). We present two models of Rudin's triangulation: a rational realization with all vertices on the boundary of the subdivided tetrahedron, and a realization with all vertices in strictly convex position.
Rudin's triangulation is strongly non-shellable: If any of its facets is removed, the remainder is not a topological ball anymore (for a thorough discussion of shellability and its applications see [1], [6] and [7, Ch.8]). It consists of 14 vertices, all on the boundary of the triangulated tetrahedron and 41 facets. In addition to being strongly non-shellable, it has an interesting property, that was first noted in [2]: The triangulation can be realized with all vertices in strictly convex position, such that the boundary is the boundary complex of a polytope. This means that there is a simplicial 3-polytope with 14 vertices which has a non-shellable triangulation without additional vertices.
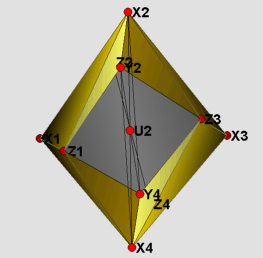
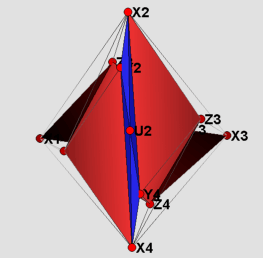
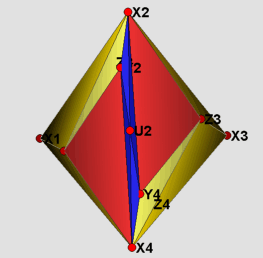
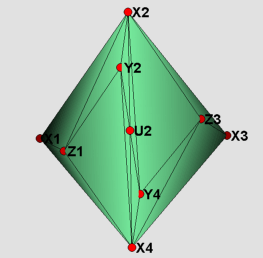
Visually, there is not much of a difference between the two models presented here. Therefore only the strictly convex realization is shown in the figures. The labeling of the vertices has been kept the same as in Rudin's paper. The visualization itself is divided into four parts. The 16 yellow tetrahedra in figure (1) form a torus. The tetrahedron with vertices Z1, Z2, Z3 and Z4 in the middle of figure (1) divides the remaining part into two congruent pieces, which are depicted in figure (2). Each of these is filled by two types of tetrahedra: those that do have U_i as one of their vertices(blue), and those that do not(red). In the main files (RudinBallRational_Main.jvx and RudinBallStrictlyConv.jvx) the different types of tetrahedra can be switched on and off using the javaview display inspector. In figure (3) the boundary of the triangulation is displayed. Finally, in figure (4) using polymake [3] we give a picture proof that the strictly convex realization is indeed a realization, such that the boundary complex is that of a polytope.
A remark concerning minimality of non-shellable 3-balls: In her original paper [5], Rudin claims that no triangulation of a 3-ball (with all vertices on the boundary) using less than 14 vertices can have the property to be non-shellable. Unfortunately she does not give a proof for this claim and it does not seem obvious how to provide one. There are examples with fewer vertices if interior vertices are permitted: A vertex-minimal example with 9 vertices and 18 facets is given by Lutz [4].
| Keywords | shellability; simplicial balls and spheres | |
| MSC-2000 Classification | 52B22 ( 57Q15) | |
| Zentralblatt No. | 05264901 |
Submitted: Thu Aug 12 19:17:58 CEST 2004.
Revised: Mon Sep 12 12:24:10 CEST 2005.
Accepted: Tue Oct 4 13:17:04 MET DST 2005.
Technische Universität Berlin
Fachbereich Mathematik, MA 6-2
Strasse des 17.Juni 136
10623 Berlin
Germany
wotzlaw@math.tu-berlin.de