

 |
 |
We present a 16-vertex triangulation of the Poincaré homology 3-sphere that can be taken as the starting point for a series of non-PL d-spheres with d+13 vertices in dimensions d≥5.
Poincaré's famous example of a non-simply connected 3-manifold with the same homology as the ordinary 3-sphere appeared in 1904 [14]. Its existence prompted the still open 3-dimensional Poincaré conjecture and had an enormous influence on the subsequent development of topology.
Poincaré obtained his example from two solid double tori identified along their boundary surfaces of genus 2. Another construction that yields the same space is due to Threlfall and Seifert. Their description of the Poincaré sphere as the spherical dodecahedron space is based on the solid dodecahedron where opposite pentagons on the boundary are identified by a coherent twist of pi/5 radians; see Threlfall and Seifert [17] or Weber and Seifert [19]. Further constructions of the Poincaré sphere are discussed in various places in the literature (cf. [9] or the references mentioned in [5]; see also [6] and [12]). The Poincaré homology 3-sphere has as its fundamental group the ``binary icosahedral group'' of order 120. It is the only Seifert homology sphere with (non-trivial) finite fundamental group [16].
Triangulations, in particular, vertex-minimal triangulations of the Poincaré sphere are interesting for the following two purposes: They can be used as reference triangulations for recognition heuristics based on so called bistellar flips as described in [5] and [12], and they can be taken as starting triangulations for the construction of non-PL d-spheres with few vertices in dimensions d≥5.
Triangulations of the Poincaré homology 3-sphere with 17 and 18 vertices were first found by Brehm (cf. [10, p. 55]) and can easily be constructed by hand; see [5]. In fact, there even are triangulations of the Poincaré homology 3-sphere with 17 vertices that have a vertex-transitive cyclic symmetry group [12].
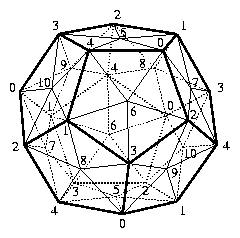
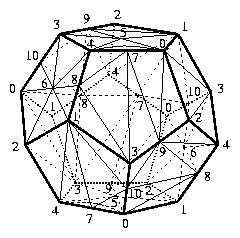
In order to obtain some small triangulation, we follow Threlfall and Seifert. We start with the solid dodecahedron and triangulate its identified boundary by introducing a midpoint for every pair of (identified) opposite pentagons. Into the interior of the dodecahedron we place an icosahedron in such a way that every vertex of the icosahedron corresponds to (a copy of) an (identified) outer pentagon. For every vertex of the icosahedron we form the cone over the respective triangulated pentagon. For every edge of the icosahedron we include the tetrahedron that is determined by this edge and the edge that separates the two corresponding neighboring pentagons. Similarly, for any triangle on the boundary of the icosahedron we take the tetrahedron that is made up by the triangle and the intersection-vertex of the three corresponding neighboring pentagons. Finally, we triangulate the interior of the icosahedron by introducing a center point and by taking the cone over the boundary of the icosahedron with respect to the center point. The resulting triangulation of the Poincaré homology 3-sphere has 5+6+12+1=24 vertices and f-vector f=(24,154,260,130). It is invariant under the 60-element group A_5 of rotations of the icosahedron and the dodecahedron.
In a next step we apply bistellar flips (which locally modify a triangulation but do not change the topological type [13]) to this triangulated manifold. In particular, we select the flips according to a simulated annealing type strategy with the objective to reduce the number of vertices of a triangulation of a manifold, which, in some cases, eventually produces a vertex-minimal triangulation; for details see [5] and [12]. An implementation of this procedure is the GAP-program BISTELLAR [11].
Theorem 1: There is a triangulation (without any symmetries) of the Poincaré homology 3-sphere on 16 vertices with f-vector f=(16,106,180,90). The 90 tetrahedra of the triangulation can be arranged to form a solid dodecahedron with 11 vertices on the (identified) boundary and with 5 additional vertices in the interior.
It follows from work of Walkup [18] that at least 11 vertices are needed for any triangulation of a 3-manifold different from S^3, S^2xS^1, or the 3-dimensional Klein bottle. For triangulations of Z_2-homology 3-spheres, other than the standard sphere, Bagchi and Datta [3] have shown recently that at least 12 vertices are necessary.
Conjecture: The triangulation of the Poincaré homology 3-sphere with f-vector f=(16,106,180,90) has the component-wise minimal f-vector for a triangulation of this manifold and is the unique triangulation with this f-vector.
In 1974, Edwards [8] proved that the double suspension of the Mazur homology 3-sphere is a topological 5-sphere. Cannon [7] later generalized this result by showing that the double suspension of any d-dimensional homology sphere is a topological (d+2)-sphere. However, for non-spherical homology d-spheres the resulting (d+2)-spheres are non-PL spheres, i.e., they are not PL-homeomorphic to the boundary of a simplex.
The standard way of suspending a space is by forming the double cone over the space. By suspending the 16-vertex triangulation of the Poincaré homology 3-sphere m≥2 times, we obtain non-PL (m+3)-spheres with 2m+16 vertices. If we instead use one-point suspensions (defined in the proof of Theorem 5.2(i) in [1], reverse operation to ``starring a vertex in an edge'' in [2], ``simplicial wedge'' in [15]), then the number of vertices can be reduced.
Theorem 2: Let d≥5. Then there are non-PL triangulations of the d-dimensional sphere on d+13 vertices.
In dimensions d≥5 every triangulated sphere with n≤d+5 vertices is a PL-sphere [4].
Question: Are there non-PL d-spheres for d≥5 with less than d+13 vertices?
We applied the program BISTELLAR to the non-PL 5-sphere with 20 vertices that we obtained from the 16-vertex triangulation of the Poincaré homology 3-sphere by standard double suspension. However, the smallest triangulation that was achieved this way has 18 vertices, so we could not improve on the question above.
Theorem 3: There is a non-PL 5-sphere with 18 vertices and f-vector f=(18,139,503,904,783,261).
Instead of the 16-vertex triangulation of the Poincaré homology 3-sphere we can, of course, take any other triangulated (non-spherical) homology 3-sphere as a starting point for a series of non-PL spheres. Triangulations of Seifert homology spheres are constructed in [6]. In fact, the Seifert homology sphere Sigma(2,3,7) with infinite fundamental group can be triangulated with 16 vertices as well. The smallest triangulation of this space that was found in [6] has f-vector f=(16,117,202,101).
| Keywords | Poincaré sphere; minimal triangulations; PL and non-PL triangulations | |
| MSC-2000 Classification | 57Q15 (57Q25) | |
| Zentralblatt No. | 05264892 |
Submitted: Tue Apr 29 12:54:13 GMT 2003.
Revised: Mon Jul 28 13:46:15 CEST 2003, Tue Aug 12 17:08:52 CEST 2003.
Accepted: Fri Aug 22 12:06:52 CEST 2003.
Royal Institute of Technology (KTH)Frank H. Lutz
Department of Mathematics
Lindstedtsvägen 25
S-10044 Stockholm
Sweden
bjorner@math.kth.se
http://www.math.kth.se/~bjorner/
Technische Universität Berlin
Fakultät II - Mathematik und Naturwissenschaften
Institut für Mathematik, Sekr. MA 6-2
Straße des 17. Juni 136
D-10623 Berlin
Germany
lutz@math.tu-berlin.de
http://www.math.tu-berlin.de/~lutz