A shellable 3-ball with a knotted spanning arc consisting of 3 edges

Author

Description

Hachimori and Ziegler [1] proved that a triangulation of a 3-ball which contains a knotted spanning arc consisting of at most 2 edges is not constructible. The following example (constructed along the ideas of Hachimori and Ziegler [1], yet considerably smaller) shows that 2 is the best possible upper bound for the number of edges.

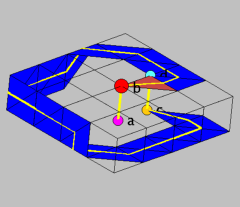
Let C₁ be the following triangulation of a pile of 4*4*1 cubes: Each cube is split into 6 tetrahedra, and the tetrahedra are all grouped around one of the diagonal axes of the cube. Furthermore let a denote the pink, b the red, c the orange and d the light blue vertex. For a face F and a vertex x let x*F denote the cone over F with apex x. The red vertex b is marked bigger since it is needed for the following: Let C := C₁ union (b*(blue faces)), then C is a shellable 3-ball because C₁ is shellable, and the arc ab-bc-cd is a knotted spanning arc of C. Since we add b*(blue faces) to C₁, the edge bc actually exists. The edges ab and cd are already contained in C₁. To visualize the knotted arc, one may imagine it as following the yellow line. Note that we do not form the cone over the dark red face adjacent to b.

Figure 1 depicts the pile of cubes and the faces needed for the construction are colored blue. The yellow line visualizes the knotted arc. To obtain the example (shel_3-ball_with_knotted_arc.jvx) one has to compleat the construction by adding b*(blue faces).

The master file shel_3-ball_with_knotted_arc.jvx contains two geometries: The facets of the 3-ball (encoded as their vertex sets) in shelling order and the knotted spanning arc (encoded as the vertex sets of its edges). In the master file point a corresponds to 25, b to 24, c to 15 and d to 14. (If needed, check the applet file for the indices of the other vertices.)

References

1. M. Hachimori and G. M. Ziegler: Decomposition of simplicial balls and spheres with knots consisting of few edges, Mathematische Zeitschrift 235 (2000), 159-171.

Files

• Master File: shel_3-ball_with_knotted_arc.jvx
• Applet File: shel_3-ball_with_knotted_arc_Applet.jvx
• Preview: shel_3-ball_with_knotted_arc_Preview.gif
• Original File (private file format): shel_3-ball_with_knotted_arc.topaz

Submission information

Submitted: Tue May 8 20:14:13 CEST 2001.
Revised: Fri Jun 14 18:18:18 CEST 2002.
Accepted: Wed Nov 20 15:58:01 CET 2002.

Author's Address

TU Berlin
Fakultät 2, Institut für Mathematik, MA 6-2
Strasse des 17. Juni 136
10623 Berlin, Germany
witte@math.tu-berlin.de