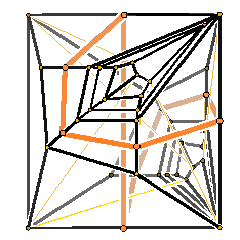
A Cubical 4-Polytope with a Dual Klein Bottle

Authors

Description

A cubical 4-polytope with a dual Klein bottle.

A d-dimensional polytope is cubical if all its facets are combinatorially isomorphic to the (d-1)-dimensional standard cube; compare [1, Sect. 4.6].

It has been observed by Stanley and by MacPherson that every cubical d-polytope P determines a normal crossing codimension one PL immersion of an abstract cubical (d-2)-manifold into (the barycentric subdivision of) the boundary of the polytope: Each vertex of the dual manifold corresponds to an edge of P and each facet separates two opposite faces of a facet of P.
In the case a of cubical 4-polytope each connected component of the dual manifold is a cubical surface (compact 2-manifold without boundary). The immersed manifold is orientable if and only if the 2-skeleton of the cubical d-polytope is ``edge orientable'' in the sense of Hetyei, that is, there is no orientation of the edges such that in each 2-face opposite edges are parallel. Hetyei conjectured that there are cubical 4-polytopes that are not edge-orientable [2, Conj. 2].

In [3] we obtain the first instance of a cubical 4-polytope (with 72 vertices and 62 facets) for which the immersed dual surface is not orientable: One of its components is a Klein bottle. This confirms Hetyei's conjecture.

This instance is constructed as follows (we refer to [3] for the details):

1. Start with two copies of the cubical octahedron (the only cubical 3-polytope with 8 facets) and glue them together such that the outcome is a polytopal 3-ball (with 2 facets) whose 2-skeleton contains a Möbius strip with parallel inner edges.
2. Both facets of this polytopal 3-ball are subdivided into cubes by the Schlegel cap construction [3]. For each of the two copies of the cubical octahedron the Schlegel cap yields a regular cubical 3-ball isomorphic to the prism over a Schlegel diagram of the cubical octahedron. The Möbius strip is not affected by the subdivision.
3. A prism construction yields a cubical 4-polytope with 72 vertices and 62 facets. One component of its immersed dual manifold is a Klein bottle.

Model produced with: polymake 1.5.1 + additional tools

References

1. B. Grünbaum: Convex Polytopes, Graduate Texts in Math. 221, Springer-Verlag, New York. Second edition by V. Kaibel, V. Klee and G. M. Ziegler (2003; original edition: Interscience, London 1967).
2. Garbor Hetyei: On the Stanley ring of a cubical complex, Discrete Comput. Geom. 14, 3 (1995), 305-330.
3. Alexander Schwartz and Günter M. Ziegler: Construction techniques for cubical complexes, odd cubical 4-polytopes, and prescribed dual manifolds (2003), Preprint, http://arxiv.org/abs/math.CO/0310269.

Files

• Master File: C4P_Klein_Master.poly
• Applet File: C4P_Klein_Applet.jvx
• Preview: C4P_Klein_Preview.gif
• Print File: C4P_Klein_Print.eps

Submission information

Submitted: Fri May 21 18:25:54 CEST 2004.
Revised: Fri Nov 19 15:19:33 CET 2004.
Accepted: Mon Nov 29 13:51:04 MET 2004.

Authors' Addresses

TU Berlin
Inst. Mathematics, MA 6-2
10623 Berlin
Germany
schwartz@math.tu-berlin.de
http://www.math.tu-berlin.de/~schwartz

TU Berlin
Inst. Mathematics, MA 6-2
Strasse des 17. Juni 136
10623 Berlin
Germany
ziegler@math.tu-berlin.de
http://www.math.tu-berlin.de/~ziegler