Uninscribable 4-Regular Polyhedron

Authors

Description

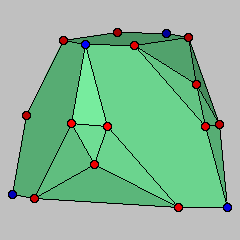
This model describes a polyhedron with four edges at each vertex, that can not be placed in convex position with all vertices on the surface of a sphere.

A convex polyhedron is said to be inscribable if there is an isomorphic convex polyhedron with all its vertices on the unit sphere, and circumscribable if there is an isomorphic convex polyhedron with all faces tangent to the unit sphere. The polar of an inscribable polyhedron is circumscribable, and vice versa.

A k-regular polyhedron is one for which each vertex has k incident edges. It is well known that there exist three-regular uninscribable polyhedra (e.g., truncate one corner from the cube) but the four-regular case is more interesting. Hodgson et al. [1] characterized the inscribable polyhedra as those having assignments of numerical weights to edges, satisfying the following constraints:

1. Each weight is strictly between 0 and 1/2.
2. The total weight at each vertex is exactly one.
3. If removing a set of edges would partition the skeleton of the polyhedron into two connected subgraphs, each of which contains more than one vertex, then that edge set must have total weight strictly greater than one.

Assigning weight 1/4 to all edges of a four-regular polyhedron polyhedron satisfies the first two constraints, and comes close to satisfying the third constraint: since all degrees are even, the skeleton of the polyhedron has an Euler tour, and this tour must cross any cut set a number of times that is an even number greater than two (if it crossed only two times, the graph would not be sufficiently connected to be a polyhedron), so any cut set in the third constraint has at least four edges and has total weight at least one. It is natural, therefore, to conjecture that all four-regular polyhedra are inscribable and dually that all polyhedra with quadrilateral facets are circumscribable. This model provides a counterexample to such a conjecture.

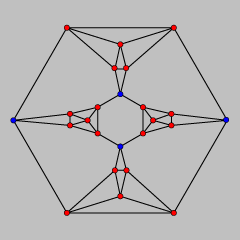
We now argue that our polyhedron can not be weighted in a way that satisfies all three constraints. In principle, the problem of finding such weights can be solved by linear programming, but in this case a simpler argument is possible. One can find a set of four vertices in the model (the vertices of a regular tetrahedron, shown in blue) the removal of which disconnects the model's skeleton into four nontrivial connected components. The total weight of the edges incident to these four vertices, by the second constraint, must equal four. Therefore, one of the four components must be connected to these vertices by edges with total weight at most one, violating the third constraint. Therefore the polyhedron is not inscribable.

References

1. Craig D. Hodgson, Igor Rivin, and Warren D. Smith: A characterization of convex hyperbolic polyhedra and of convex polyhedra inscribed in the sphere, Bull. Amer. Math. Soc. (N.S.) 27 (1992), 246-251, http://arxiv.org/abs/math.MG/9210218.

Files

• Master File: uninscribable_Master.poly
• Applet File: uninscribable_Applet.jvx
• Preview: uninscribable_Preview.gif
• Image: uninscribable_Schlegel.gif

Submission information

Submitted: Fri Aug 15 00:34:19 CEST 2003.
Accepted: Wed Mar 10 09:12:35 CET 2004.

Authors' Addresses

Univ. of California, Irvine
School of Information and Computer Science
Irvine, CA 92697-3425
USA
eppstein@ics.uci.edu
http://www.ics.uci.edu/~eppstein/

Univ. of California, Irvine
School of Information and Computer Science
Irvine, CA 92697-3425
USA
dillenco@ics.uci.edu
http://www.ics.uci.edu/~dillenco/