Ambiguous Incidences of Unbounded Polyhedra

Authors

Description

In general, the face lattice of an unbounded polyhedron cannot be recovered from its vertex-facet incidences as one sees from the examples of polyhedral cones. Here we provide a ``more convincing'' four-dimensional example (appearing in [1]) for the ambiguity of vertex-facet incidences in the following sense: the polyhedra in this example have the property, that the vertex sets of facets form an anti-chain in the Boolean poset (i.e., they form a clutter) - while for cones all facets have the same set of vertices; the set of vertices is full-dimensional - while for a cone the set of vertices has dimension 0; and they have finite facets - while the only finite face of a cone is its apex.

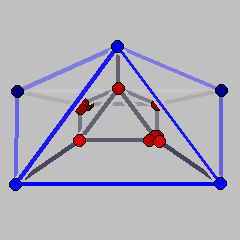
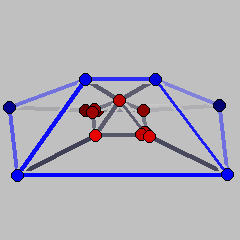
In order to construct the example, we start with the cartesian product Q of an ordinary three-dimensional pyramid over a square and a ray. Thus, Q is a four-dimensional polyhedron with one bounded facet (the three-pyramid we started from), one facet which is an infinite prism over a square, and four facets that are infinite prisms over triangles. From the vertex v which comes from the top of the pyramid one single extremal ray eminates. If we now slightly tilt one of the facets that meet in v, we will not change the vertex-facet incidences of the polyhedron, but we will create a second extremal ray that eminates fom v. To make the vertex sets of facets an anti-chain and to ensure that the convex hull of the vertices is full-dimensional, we additionally cut off two opposite vertices of the base of the pyramid.

The files P1.poly and P2.poly below are polymake files containing coordinate descriptions of these two polyhedra. Notice that, in order to obtain finite Schlegel diagrams, both files contain an artificial facet, where the polyhedron is projected on. This corresponds to the inequality x₄<=20 which is the last facet listed in both cases. The artificial facets are colored blue in the Schlegel diagrams; the blue vertices correspond to infinite rays.

Model produced with: polymake 1.3.1

References

1. Ewgenij Gawrilow and Michael Joswig: polymake, http://www.math.tu-berlin.de/diskregeom/polymake.
2. Michael Joswig, Volker Kaibel, Marc E. Pfetsch, and Günter M. Ziegler : Vertex-Facet Incidences of Unbounded Polyhedra (2000), preprint.

Files

• Master File: P1.poly
• Master File: P2.poly
• Applet File: P1.jvx
• Applet File: P2.jvx
• Preview: P1.gif
• Preview: P2.gif

Submission information

Submitted: Mon May 1 09:32:05 CET 2000.
Accepted: Mon Nov 20 17:06:57 CET 2000.

Authors' Addresses

Technische Universität Berlin
Fachbereich Mathematik, MA 7-1
Straße des 17. Juni 136
10623 Berlin, Germany
joswig@math.TU-Berlin.DE
http://www.math.TU-Berlin.de/~joswig/

Technische Universität Berlin
Fachbereich Mathematik, MA 7-1
Straße des 17. Juni 136
10623 Berlin, Germany
kaibel@math.TU-Berlin.DE
http://www.math.TU-Berlin.de/~kaibel/

Technische Universität Berlin
Fachbereich Mathematik, MA 7-1
Straße des 17. Juni 136
10623 Berlin, Germany
pfetsch@math.TU-Berlin.DE
http://www.math.TU-Berlin.de/~pfetsch/

Technische Universität Berlin
Fachbereich Mathematik, MA 7-1
Straße des 17. Juni 136
10623 Berlin, Germany
ziegler@math.TU-Berlin.DE
http://www.math.TU-Berlin.de/~ziegler/