

 |
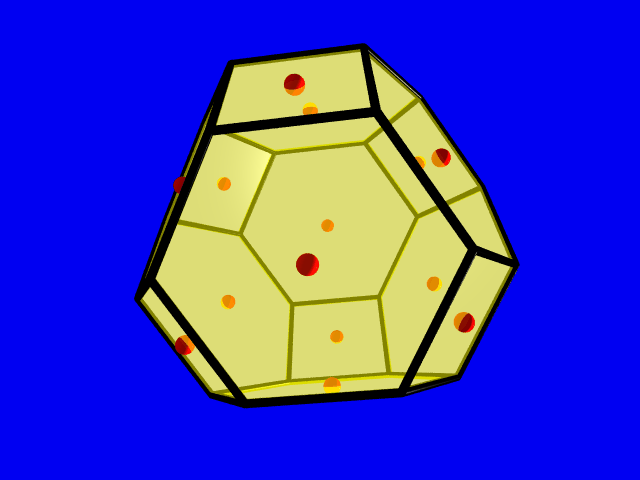
Densest lattice packing of truncated octahedron
The truncated octahedron has 24 vertices, 36 edges and 14 facets, 8 hexagons and 6 squares. It is one of the thirteen Archimedean solids and its dual is called tetrakis hexahedron. It was rediscovered during th 15th century by the outstanding artist Piero della Francesca.
Since the truncated octahedron belongs to the family of spacefillers (more precisely, to the class of primitive parallelohedra) the density of a densest lattice packing is 1. The 14 points in the pictures show the lattice point of a critical lattice lying in the boundary.
Model produced with: JavaView v2.00.a11
| Keywords | lattice packings; polytopes; packings; critical lattice; truncated octahedron | |
| MSC-2000 Classification | 52C17 (11H31) | |
| Zentralblatt No. | 01683008 |
Gif-file was produced by Povray 3.02
Submitted: Thu Feb 1 16:41:52 CET 2001.
Accepted: Fri Apr 27 14:11:54 CET 2001.
University of Magdeburg
Department of Mathematics
Universitätsplatz 2
D-39106 Magdeburg
henk@mail.math.uni-magdeburg.de
http://www.math.uni-magdeburg.de/~henk