

 |
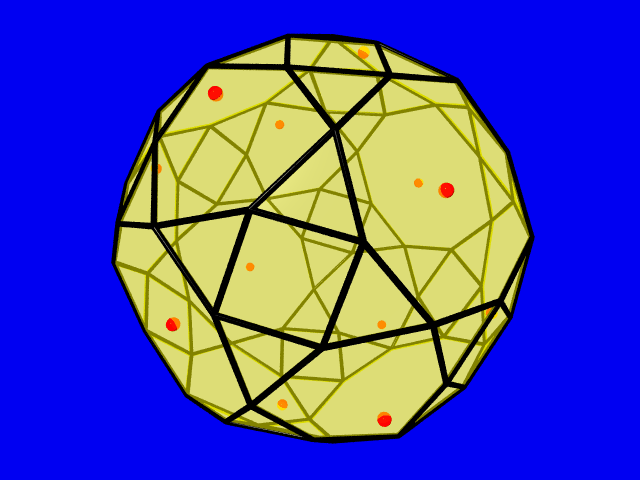 |
Densest lattice packing of a snub cube
The snub cube has 24 vertices, 60 edges and 38 facets, 6 squares and 32 triangles. It is one of the thirteen Archimedean solids and its dual is called pentagonal icositetrahedron. Maybe the first presentation of this polytope can be found in the revised version of Albrecht Dürer's Underweysung der Messung (around 1538).
The density of a densest lattice packing was calculated with the algorithm of Betke and Henk. Since the snub cube is a non 0-symmetric polytope one first has to compute the difference body of a snub cube, which is a 0-symmetric polytope with 72 vertices, 144 edges and 74 facets, 6 octagons, 8 hexagons, 12 squares and 48 triangles. It is shown in the second picture.
The optimal packing lattices of a convex body and its difference body coincide. The lattice packing density of a snub cube is equal to 0.7876..., and the 12 points in the picture show the lattice points of a critical lattice of the difference body lying in the boundary.
Model produced with: JavaView v2.00.a11
| Keywords | lattice packings; polytopes; packings; critical lattice; snub cube | |
| MSC-2000 Classification | 52C17 (11H31) | |
| Zentralblatt No. | 01683000 |
Gif-file was produced by Povray 3.02
Submitted: Thu Feb 1 16:41:52 CET 2001.
Accepted: Fri Apr 27 14:11:54 CET 2001.
University of Magdeburg
Department of Mathematics
Universitätsplatz 2
D-39106 Magdeburg
henk@mail.math.uni-magdeburg.de
http://www.math.uni-magdeburg.de/~henk