Truncated Dodecahedron

Author

Description

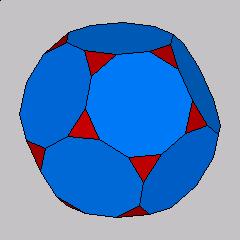
The truncated dodecahedron is one of the thirteen Archimedean solids.

The truncated dodecahedron has 60 vertices, 32 faces and 90 edges. It is generated by truncating the vertices of a dodecahedron such, that the faces of the dodecahedron are cut to regular dakagons. Here the distance from vertex to center point is scaled to 1; the edge-length is 2sqrt((37-15sqrt(5))/122).

The coordinates of the truncated dodecahedron where computed with polymake. The planes with normals showing to the icosahedron vertices with distance sqrt((25+8sqrt(5))/61) and the planes with normals showing to the dodecahedron with distance sqrt((109+30sqrt(5))/183) to the center point where intersected, the 60 intersection points are the vertices of the truncated dodecahedron.

Model produced with: JavaView 2.00.005

References

1. H. S. M. Coxeter: Regular Polytopes, Collier-Macmillan Ltd. London (1963).
2. Magnus J. Wenniger: Polyhedron Models, Cambridge University Press (1970).
3. Alan Holden: Shape, Space and Symmetry, Columbia University Press New York/London (1971).
4. Michael Joswig, Ewgenij Gawrilow: Polymake, http://www.math.tu-berlin.de/diskregeom/polymake/doc/.
5. Konrad Polthier and Samy Khadem and Eike Preuss and Ulrich Reitebuch: JavaView Home Page, http://www.javaview.de/.

Files

• Master File: truncateddodecahedron_Master.jvx
• Applet File: truncateddodecahedron_Master.jvx
• Preview: truncateddodecahedron_Preview.gif
• Original File (private file format): truncateddodecahedron_Original.poly

Submission information

Submitted: Fri Sep 1 16:24:12 MET 2000.
Accepted: Thu Oct 25 14:19:08 MDT 2001.

Author's Address

Technische Universität Berlin
Fachbereich Mathematik, MA 8-5
Straße des 17. Juni 136
D-10623 Berlin, Germany
fuli@sfb288.math.tu-berlin.de
http://www-sfb288.math.tu-berlin.de/~fuli/